今天,学霸们为大家整理了一份高中数学老师都推荐的数学解题方法。这21种方法涵盖了高中数学的方方面面,可以说是高中数学解题方法的全面汇总。各位同学记得分享给小伙伴们,一起学习,更高效哦!
1. 解决绝对值问题
绝对值问题主要包括化简、求值、方程、不等式、函数等题型。基本思路是:将含绝对值的问题转化为不含绝对值的问题。具体的转化方法有:
- 分类讨论法:根据绝对值中的数或式子的正、零、负情况去掉绝对值。
- 零点分段讨论法:适用于含一个字母的多个绝对值的情况。
- 两边平方法:适用于两边非负的方程或不等式。
- 几何意义法:适用于有明显几何意义的情况。
2. 因式分解
因式分解的技巧在于根据项数选择方法并按一般步骤顺利进行。因式分解的一般步骤包括:
- 提取公因式- 选择用公式- 十字相乘法- 分组分解法- 拆项添项法
3. 配方法
利用完全平方公式将一个式子或部分化为完全平方式的方法称为配方法。配方法在数学中非常重要,主要依据有:
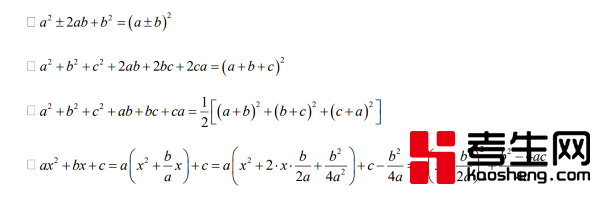
4. 换元法
解某些复杂的特型方程时,可以使用换元法。换元法解方程的一般步骤是:
- 设元- 换元- 解元- 还元
5. 待定系数法
待定系数法在已知对象形式的条件下求对象的一种方法,适用于求点的坐标、函数解析式、曲线方程等问题。其解题步骤是:
- 设- 列- 解- 写
6. 复杂代数等式
复杂代数等式条件的使用技巧包括:左边化零,右边变形。
- 因式分解型:(-----)(----)=0 两种情况为或型
- 配成平方型:(----)^2 (----)^2=0 两种情况为且型
7. 数学中两个最伟大的解题思路
- 求值的思路:列欲求值字母的方程或方程组
- 求取值范围的思路:列欲求范围字母的不等式或不等式组

8. 化简二次根式
基本思路是:把√m化成完全平方式。即:

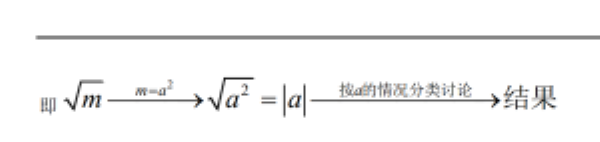
9. 观察法
通过观察法可以直接看出题目中的规律和解题思路。

10. 代数式求值
求代数式值的方法有:
- 直接代入法
- 化简代入法
- 适当变形法(和积代入法)
注意:当求值的代数式是字母的“对称式”时,通常可以化为字母“和与积”的形式,从而用“和积代入法”求值。
11. 解含参方程
含参方程中除未知数外还包含其它字母,称为参数。解含参方程通常用‘分类讨论法’,其原则是:
- 按照类型求解
- 根据需要讨论
- 分类写出结论
12. 恒相等成立的有用条件

13. 恒不等成立的条件
由一元二次不等式解集为$\mathbb{R}$的有关结论,可以得到恒不等成立的条件。

14. 平移规律
图像的平移规律是研究复杂函数的重要方法。平移规律为:
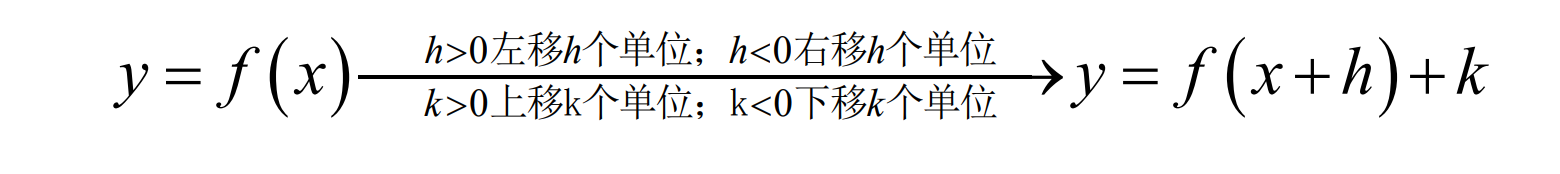
15. 图像法
图像法是讨论函数性质的重要方法,具体包括:

16. 函数、方程、不等式的重要关系

17. 一元二次方程的解法
一元二次不等式可以用因式分解转化为二元一次不等式组去解,但更简便的解法是根据二次函数的图像去解。具体步骤如下:
- 化二次为正- 判别且求根- 画出示意图- 解集横轴中







